Что такое точки Лагранжа?
Содержание страницы
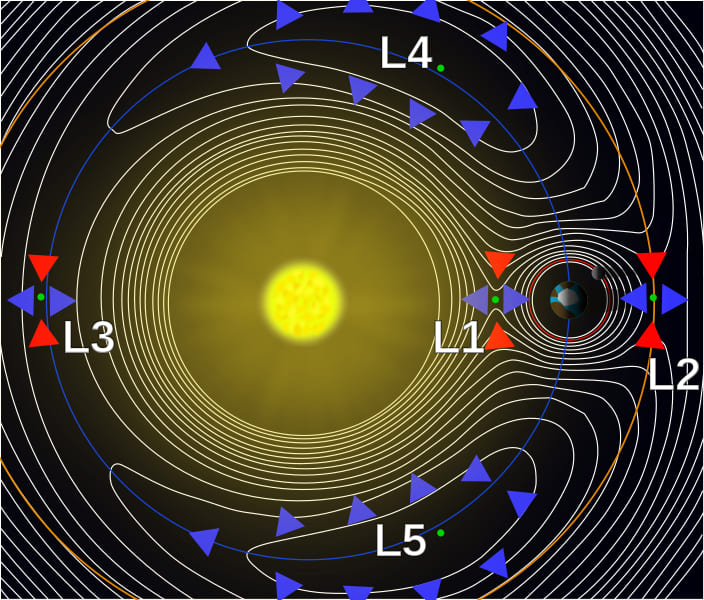
Точки Лагранжа — это области равновесия, в которых совместное гравитационное поле двух массивных тел аннулируется центробежной силой, ощущаемой третьим, гораздо меньшим объектом, так что третий объект находится в состоянии покоя относительно двух больших тел.
Около полувека назад, до того как люди задумались о терраформировании Марса или Луны для проживания людей, энтузиастов космических поселений привлекала другая идея. Идея космических колоний возникла в 1970-х годах, когда физик Джерард О’Нил выдвинул концепцию орбитальной среды обитания, которая будет занимать относительно стабильные точки в космосе, называемые точками Лагранжа.
Начнем с того, что если бы вы смогли найти правильную точку между Луной и Землей, то туда можно было бы поместить объект относительно небольшой массы, и он оставался бы там неопределенное время, облетая вокруг Земли синхронно с Луной.
Что такое точки Лагранжа?
Гравитационные силы, действующие на два массивных объекта в одной точке, обычно не уравновешиваются, изменяя орбиту любого объекта, находящегося в этой точке.
Однако точки Лагранжа — это области равновесия, в которых суммарное гравитационное поле двух массивных (небесных) тел нивелируется центробежной силой, которую испытывает третий, гораздо меньший объект, так что чистая сила на третье тело равна нулю.
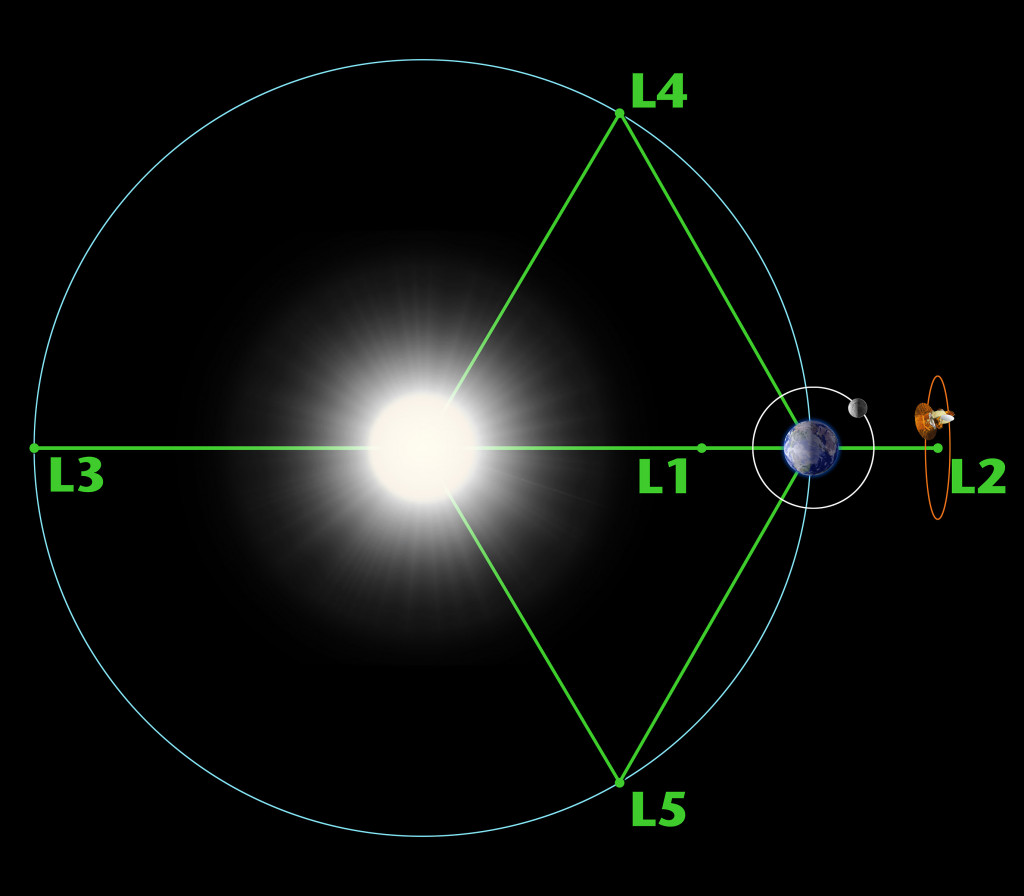
Поэтому, оказавшись в точке равновесия, относительно маломассивный объект будет иметь нулевую массу и ускорение (относительно более тяжелых тел), то есть будет находиться в состоянии покоя. Существует пять точек вокруг звезды или небесного тела, в которых все силы находятся в равновесии.
Эти точки, называемые также точками равновесия, не фиксированы в пространстве, но фиксированы относительно двух основных тел. Для системы Земля-Луна точки перемещаются вместе с центром тяжести Земли-Луны с тем же периодом, что и Луна.
Математика, которая помогла решить проблему трех тел
Пока только Земля и Луна движутся навстречу друг другу, Луна будет продолжать двигаться по очень специфической траектории, которую можно описать математически с большой точностью. Но что происходит, когда в эту смесь добавляется третье тело?
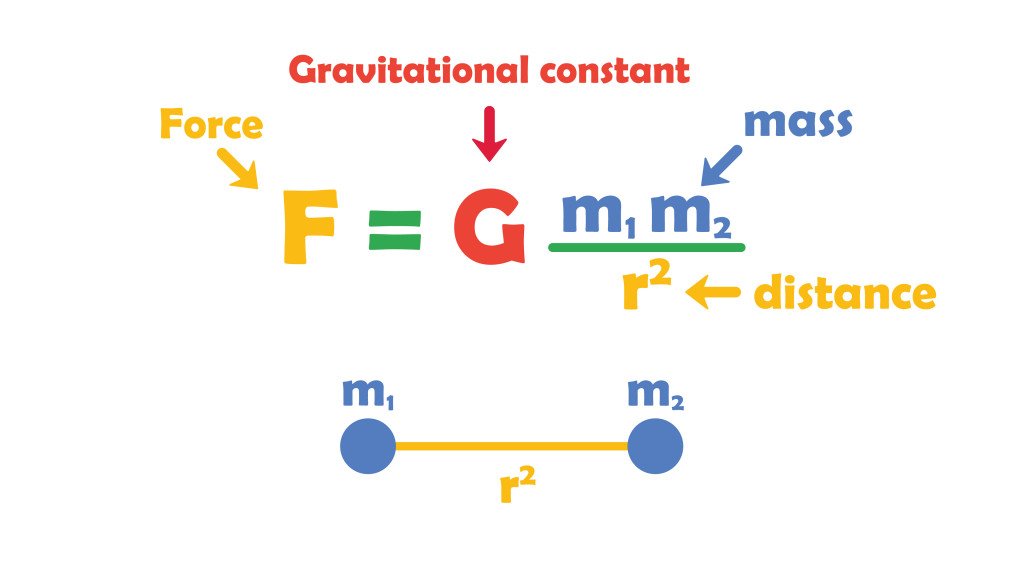
Задача трех тел заключается в том, чтобы вычислить, где находятся три небесных тела, взаимодействующие посредством гравитации (сила обратного квадрата), по отношению друг к другу с течением времени (т.е. движения). Однако, поскольку пространство не пустое, и на все вокруг действуют сразу несколько сил, система, состоящая из трех тел, в конечном итоге хаотична, и точное поведение тел невозможно предсказать.
Если для задачи о двух телах Ньютону удалось найти общее решение, то решение задачи о трех телах оказалось гораздо более сложной задачей. Когда появилось третье тело, проблема стала намного сложнее. Исследования Пуанкаре показали, что детерминированного решения задачи трех тел, возможно, не существует.
Космический телескоп Джеймса Уэбба (JWST) в точке L2 Солнца-Земли и климатическая обсерватория глубокого космоса (DSCOVR) в точке L1 могут поддерживаться там с минимальным расходом топлива и незначительными корректировками. Некоторые другие космические обсерватории, такие как «Гершель» и «Планк» (для предельно точного измерения CMB), а также «Гайя» (для картирования положения и скоростей миллиарда звезд с целью изучения истории Млечного пути), также находятся на орбите Солнце-Земля L2.
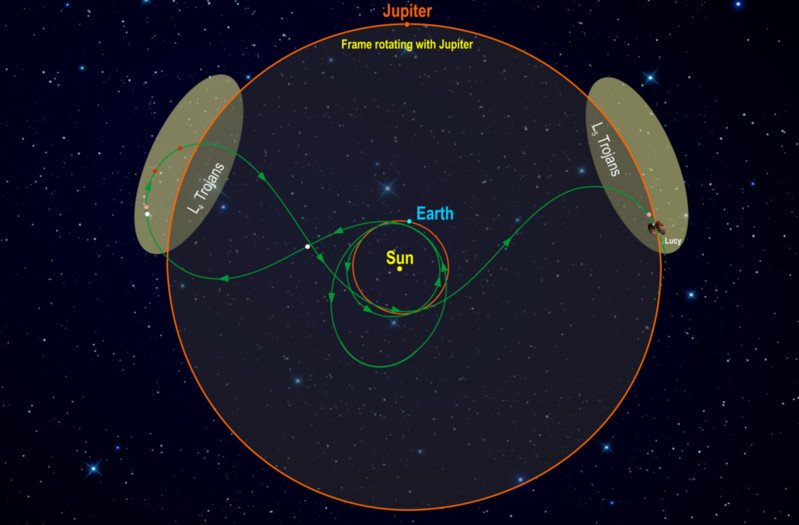
В системе Солнце-Юпитер более 7 000 астероидов группируются вокруг гравитационно стабильных точек Лагранжа L4 и L5. Называемые троянцами, эти астероиды в целом сгруппированы в два роя — один предшествует газовому гиганту, а другой следует за ним по орбите вокруг Солнца.
Ученые предположили, что области Лагранжа могут таить в себе еще не открытые планетные тела или даже обломки древних внеземных космических кораблей. Поскольку точки Лагранжа возникают в пространстве, где две или более противоположные силы уравновешены, если бы космический корабль мог генерировать силу, противодействующую гравитации, можно было бы создать искусственные точки равновесия в пространстве, чтобы космический корабль мог висеть практически в любой точке космоса без необходимости постоянно следовать по определенной орбите. Для этого можно было бы использовать солнечные паруса, использующие солнечный свет для движения.
Несомненно, миссии к точкам Лагранжа могут быть использованы как ступеньки на пути к более глубокому исследованию космоса.