Открытие: «чистая математика» является частью эволюционной генетики

Исследователи выявили взаимосвязь между теорией чисел и эволюционной генетикой, предположив, что чисто математические принципы могут влиять на биологию. Это открытие, основанное на фенотипической устойчивости, показывает, что генотипы могут быть организованы в соответствии с математическими закономерностями. Эта перспектива открывает новое направление исследований, указывая на то, что чистая математика может быть более неразрывно связана с жизнью, чем считалось ранее.

Слияние математики и биологии всегда было источником вопросов и исследований для исследователей. В частности, в последнее время на первый план вышла такая область, как эволюция. Исследователи из Королевского общества заинтересовались фенотипической устойчивостью. Это средняя мутационная устойчивость всех генотипов, связанных с данным фенотипом. Она важна для понимания механизмов, лежащих в основе появления новых фенотипических вариаций в эволюционирующей популяции.

Авторы предполагают, что сама природа может управляться чисто математическими принципами, что является удивительной связью между теорией чисел и эволюционной генетикой. Работа опубликована в Journal of The Royal Society Interface.

Когда теория чисел встречается с биологией

Теория чисел, традиционно ассоциирующаяся с чисто математическими областями, нашла неожиданное применение в эволюционной биологии. Исследователи использовали эту теорию для изучения фенотипической устойчивости — важнейшей характеристики для понимания того, как организмы эволюционируют в условиях мутаций. Они обнаружили, что эта устойчивость достигает своего пика, когда генотипы, являющиеся генетическими кодами организма, структурированы в соответствии с особой моделью, называемой «графами каменщика». Это название происходит от того, что они строятся путем многократного добавления соседней вершины к графу Хэмминга (математическое понятие, используемое для измерения расстояний между последовательностями кодов), что напоминает процесс укладки кирпичей.

Но еще более интересным является то, что максимальное значение этой фенотипической устойчивости определяется очень специфической математической функцией. Эта функция является фрактальной, то есть имеет повторяющиеся паттерны в различных масштабах. Она непрерывна, то есть в ней нет прерываний, но у нее есть одна особенность: она не дифференцируема ни в одной точке. Другими словами, она настолько сложна и нерегулярна, что ее наклон невозможно вычислить ни в одной точке. Эта функция, хотя и полученная из теории чисел, может стать ключом к пониманию того, как природа оптимизировала способность организмов эволюционировать и адаптироваться к окружающей среде.

Глубокие последствия для биологии

Профессор Ард Луис из Оксфордского университета, возглавивший исследование, поясняет в пресс-релизе: «Мы уже давно знаем, что многие биологические системы демонстрируют удивительно высокую фенотипическую устойчивость, без которой эволюция была бы невозможна«. Но ученые не знали, каков абсолютный максимум устойчивости и существует ли вообще такой максимум. Именно на этот вопрос и попыталась ответить группа исследователей.

Для этого исследователи опирались на карты генотип-фенотип. Они являются важнейшим инструментом в биологии для понимания того, как генетические вариации (генотипы) преобразуются в наблюдаемые характеристики (фенотипы). В частности, вторичная структура РНК — это пространственная конфигурация РНК, которая играет важнейшую роль в ее функционировании и регуляции. Аналогичным образом, сворачивание белков, подчиняющееся гидрофобно-полярной модели (ГП), определяет трехмерную форму белков, которая необходима для их функционирования.

Рассматривая эти карты вторичной структуры РНК и модель ГП, мы видим, что они могут демонстрировать фенотипическую устойчивость, которая достигает верхнего предела, определяемого упомянутыми выше математическими принципами.

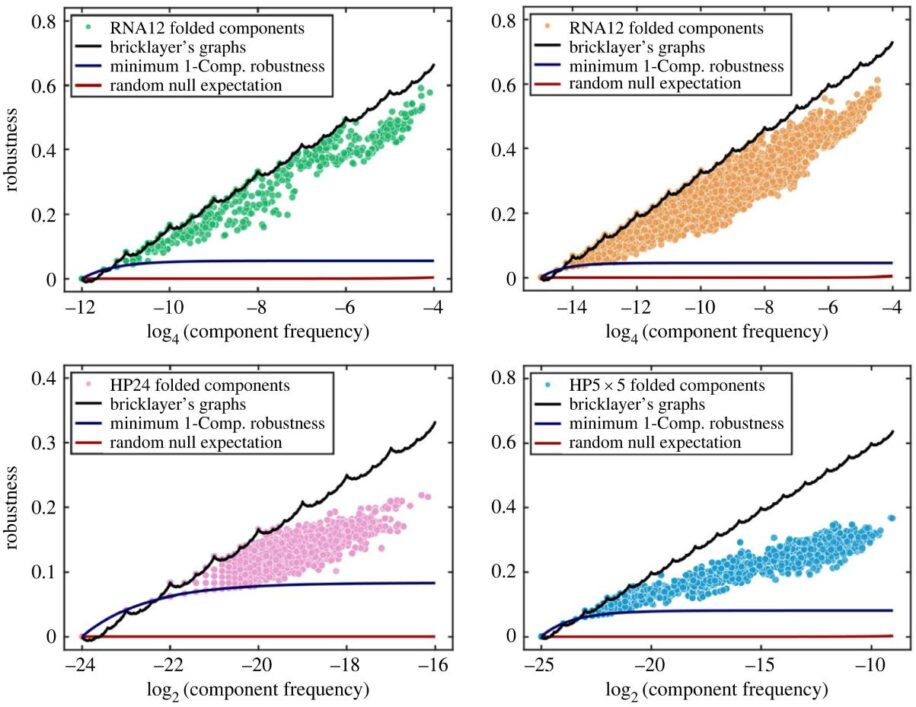
Затем они доказали, что максимальная устойчивость пропорциональна логарифму доли всех возможных последовательностей, соответствующих фенотипу, с поправкой, которую дает функция суммы цифр sk(n), определяемая как сумма цифр натурального числа n в основании k. Например, для n = 123 по основанию 10 сумма цифр будет равна s10(123) = 1 + 2 + 3 = 6.

Ведущий автор доктор Вайбхав Моханти (Гарвардская медицинская школа) говорит: «Самое удивительное, что при картировании последовательностей вторичных структур РНК мы обнаружили четкие доказательства того, что природа в некоторых случаях достигает предела точной максимальной устойчивости«.

Многообещающее будущее для исследований

Этот вывод позволяет предположить, что природа в своем стремлении к оптимизации может принимать генетические конфигурации, соответствующие точным математическим моделям. Другими словами, математические принципы — это не просто аналитические инструменты, они могут быть неразрывно связаны с тем, как эволюционирует и адаптируется жизнь. Это позволяет по-новому взглянуть на традиционное понимание эволюционной биологии и предположить, что математика может лежать в самом сердце механизмов эволюции.
Такое слияние биологии и математики открывает путь к новым методам исследования и лучшему пониманию эволюции. Распознав математические закономерности, лежащие в основе генетики, ученые теперь могут предложить новые подходы к изучению эволюции и, возможно, даже повлиять на нее.