Классические компьютеры неразрывно ассоциируются сцифровой электроникой. Цифровой подход основан напредставлении информации ввиде единиц инулей. Такой подход естественен при сложении или вычитании целых идаже рациональных чисел. Онже применяется ипри обработке аналоговых сигналов, которые представляют собой функции одной или нескольких переменных. Вэтом случае необходимо производить аналогово-цифровые преобразования.
Впоисках способов ускорения вычислений физики иинженеры все чаще стали смотреть всторону аналоговых компьютеров. Этому способствует бурный прогресс вобласти создания материалов, по-новому взаимодействующих сосветом. Например, мыуже рассказывали, как ученые создалиоптическиеитерагерцовыеаналоговые нейронные сети. Ключевым недостатком этих технологий стал ихбольшой размер, что непозволяет реализовать ихначипе.
Аналоговые компьютеры используются в другом подходе к вычислениям. Внем обработка аналоговой информации производится напрямую. Благодаря этому аналоговый подход обладает преимуществом вскорости при работе сфункциями, например, дифференцировании, интегрировании или решении дифференциальных уравнений. Строго говоря, первые вычислительные машины были именно аналоговыми, вчастности, механическими. Ихключевым недостатком стало отсутствие универсальности, и, вконце концов, вовторой половине ХХ века аналоговые компьютеры уступили своё место цифровым устройствам, чья вычислительная мощность на тот момент росла согласнозакону Мура.
Американские физики спроектировали компактный оптический аналоговый вычислитель, который практически мгновенно решает дифференциальные иинтегральные уравнения. Вего основе лежит метаматериал ссубволновым распределением диэлектрической проницаемости, арешение кодируется врассеянной нанем волне. ИсследованиеопубликовановPhysical Review Letters.
Для решения этой проблемы Андреа Алу (Andrea Alù) сколлегой изГородского университета Нью-Йорка предложили использовать метаматериалы. С помощью численных симуляций они показали, что сконструированные наихоснове микрометровые аналоговые вычислители способны почти мгновенно решать дифференциальные иинтегро-дифференциальные уравнения свысокой точностью иустойчивостью, если облучать ихсветом определенной частоты.
Некоторые математические операции проще проводить водну сторону, чем вдругую. Типичный пример— это дифференцирование или интегрирование. Напрактике мычаще всего сталкиваемся снеобходимостью восстановить исходные данные понабору наблюдаемых данных, произведя вычисления в«сложную» сторону. Решение такихобратных задачзанимает важное место вцелом ряде прикладных наук.
Применение оптического аналогового вычислителя кэтой проблеме основано напредставлении входных ивыходных решений ввиде разложения поимпульсам. Вычислитель проектируется таким образом, чтобы связать эти коэффициенты согласно некоторому оператору, который содержит всебе всю информацию озадаче. Для реализации напрактике невозможно сохранить бесконечность такого разложения: его приближенность должна быть сбалансирована стребуемой точностью восстановления.
Авторы предложили использовать вкачестве входных ивыходных данных электромагнитные волны, которые рассеиваются вычислителем, представляющим собой структуру, чья диэлектрическая проницаемость зависит откоординаты некоторым заранее настроенным образом. Ихзадачей было описать профиль этой структуры взависимости оттого, какое уравнение вычислитель будет решать.
Для демонстрации работоспособности этого принципа, физики ограничились двумерным представлением. Оно предполагает, что все волны имеют цилиндрический волновой фронт, адиэлектрическая проницаемость зависит только отдвух координат. Выбрав поляризацию волн, перпендикулярную плоскости, авторы свели электромагнитную задачу кскалярной. Вэтом случае входные ивыходные данные имели вид одномерных функций полярного угла.
Исследователи раскладывали рассеянные ипадающие волны пофункциям Ханкеля первого ивторого рода, соответственно. Это позволило описывать данные ввиде столбцов, асамо математическое преобразование ввиде матрицы. Для того чтобы сопоставить этой матрице некоторое распределение диэлектрической проницаемости, физики решали задачу оптимизации для целевой функции, собранной изошибок преобразования для всех компонент разложения.
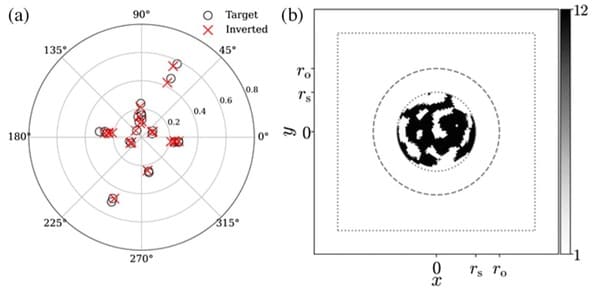
Вкачестве примера физики спроектировали вычислитель, который решает дифференциальное уравнение второго порядка, атакже интегральное уравнение Фредгольма второго рода. Вихмодели рабочая частота волн, раскладываемых попяти гармоникам, составила 135терагерц, радиус структуры был равен одному микрометру, аинформация считывалась срадиуса, равного 1,6микрометра. Врезультате вычислений они восстанавливали пространственный профиль для диэлектрических проницаемостей, равный 1и12. Работоспособность профиля авторы проверяли методом конечных элементов, сравнивая волны навыходе сточным решением уравнений.
Результаты симуляций показали, что сделанных приближений достаточно для хорошего воспроизведения решений. Модель показала устойчивость даже тогда, когда авторы добавили шум кчастоте икраспределению диэлектрической проницаемости. Физики отмечают, что если расширить описанный метод дотрехмерного случая, это позволить решать задачи для двумерных функций. Вданный момент они работают над экспериментальной реализацией предложенного аналогового вычислителя врамках оптики и акустики.
НиТ писал про новый метаматериал, который сможет увеличивать мощность роботов без необходимости в подпитке их дополнительной энергией.


